The Hidden Risks in the Hierarchical Risk Parity-Part 1
Hi quants and enthusiasts, today I would like to bring you a look at the hidden risks in ML portfolios.
The Hierarchical Risk Parity (HRP) approach has become quite famous and rightly so because of its allocation proposal. This allocates the optimal weights through clusters, based on a hierarchy in the set of assets. This will be a series of short posts demystifying some of the myths about clustering and portfolio allocation.
Recent literature has accounted for the dangers of misspecification of the covariance matrix, as you can see here.
The experiment performed here was simple. We made the simulation of the three assets, without codependency between them, and with skew-t distribution. The only point here is that asset two was generated with the smallest conditional variance and also with decreasing ARMA mean.
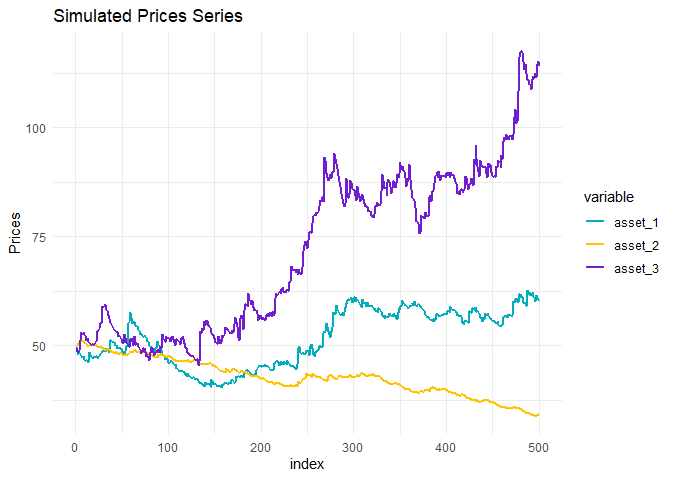
Here is a little tease: You find the optimal weights in your portfolio given by the HRP using single linkage according to the table below, the weights were estimated considering the last two years of trade, what to do?
| Asset | Weight |
|---|---|
| 1 | 11% |
| 2 | 84% |
| 3 | 5% |
The first lesson about HRPs is that returns are not considered here, and when we have assets without codependency, each asset tends to become a single cluster. And so these assets will receive a greater weight, depending on the total number of clusters and how many assets each cluster contains.